Updated Dec 10, 2020
This page is out-of-date. Visit the updated version of this page on our wiki.
Among two animals and nine machines:
- In terms of mass⋅distance/energy, the most efficient animal was 2-8x more efficient than the most efficient machine. All entries fell within two orders of magnitude.
- In terms of distance/energy, the most efficient animal was 3,000-20,000x more efficient than the most efficient machine. Both animals were more efficient than all machines. Entries ranged over more than eight orders of magnitude.
Details
Background
This case study is part of research that intends to compare the performance of human engineers and natural evolution on problems where both have developed solutions. The goal of this is to inform our expectations about the performance of future artificial intelligence relative to biological minds.
Metrics
We consider two metrics:
- Distance per energy used (meters / kilojoule).
- Mass times distance per energy used (kilograms⋅meters / joule).
These operationalize the problem of flight into two more specific problems. There are many other aspects of flight performance that one could measure, such as energy efficiency of acceleration in a straight line, turning, hovering, vertical acceleration, vertical distance, landing, taking off, time flying per energy, and our same measures with fewer or further restrictions on acceptable entries. For instance, we might look at the problem of flying with flapping wings, or without the restriction that the solutions we consider are heavier than air and self powered.
We did not require that the flight of an entry be constantly powered. Solutions that spend some time gliding as well as some time using powered flight were allowed. Both albatrosses and butterflies use air currents to fly further.1 The energy gains from these techniques were not included in the final score, and entries were not penalized for spending a larger fraction of time gliding. It seems likely that paramotor pilots use similar techniques, since paramotors are well suited to gliding (being paragliders with propeller motors strapped to the backs of their pilots). Our energy efficiency estimate for the paramotor came from a record breaking distance flight in which the quantity of available fuel was limited, and so it is likely that some gliding was used to increase the distance traveled as much as possible.
When multiple input values could have been used, such as the takeoff weight and the landing weight, or different estimates for the energetic costs of different kinds of flight for the Monarch butterfly, we generally calculated a high and a low estimate, taking the most optimistic and pessimistic inputs respectively. In all cases, the resulting best and worst estimates differed by less than a factor of ten.
Selection of case studies
We selected case studies informally, according to judgments about possible high energy efficiencies, and with an eye to exploring a wider range of case studies.
We started by looking at the Boeing 747-400 plane, the Wandering Albatross, and the Monarch Butterfly. We chose the animals for both being known for their abilities to fly long distances, and for both having fairly different body plans.
All three scored surprisingly similarly on distance times weight per energy (details below). This prompted us to look for engineered solutions that were optimized for fuel efficiency. To that end, we looked at paramotors and record breaking flying machines. In the latter category, we found the MacCready Gassomer Albatross, which was a human powered flying device that crossed the English Channel, and the Spirit of Butts’ Farm, which was a model airplane that crossed the Atlantic on one gallon of gasoline.
For reasons that are now obscure, we also included a number of different planes.
We would have liked to include microdrones, since they are different enough from other entries that they might be unusually efficient. However we did not find data on them.
Case studies
These are the full articles calculating the efficiencies of different flying machines and animals:
- Wright Flyer
- Wright model B
- Vickers Vimy
- North American P-51 Mustang
- Paramotors
- The Spirit of Butt’s Farm
- Monarch butterfly
- MacCready Gossamer Albatross
- Airbus A-320
- Boeing 747-400
- Wandering albatross
Summary results
Results are available in Table 1 below, and in this spreadsheet. Figures 1 and 2 below illustrate the equivalent questions of how far each of these animals and machines can fly, given either the same amount of fuel energy, or fuel energy proportional to their body mass.
| Name | natural or human-engineered | kg⋅m/J | m/kJ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| worst | mean | best | worst | mean | best | ||||
| Monarch Butterfly | natural | 0.065 | 0.21 | 0.36 | 100000 | 350000 | 600000 | ||
| Wandering Albatross | natural | 1.4 | 2.2 | 3 | 240 | 240 | 240 | ||
| The Spirit of Butt’s Farm | human-engineered | 0.086 | 0.12 | 0.16 | 32 | 32 | 32 | ||
| MacGready Gossamer Albatross | human-engineered | 0.19 | 0.32 | 0.46 | 2 | 3.3 | 4.6 | ||
| Paramotor | human-engineered | 0.058 | 0.079 | 0.1 | 0.36 | 0.36 | 0.36 | ||
| Wright model B | human-engineered | 0.036 | 0.078 | 0.12 | 0.1 | 0.16 | 0.21 | ||
| Wright Flyer | human-engineered | 0.022 | 0.042 | 0.061 | 0.080 | 0.13 | 0.18 | ||
| North American P-51 Mustang | human-engineered | 0.25 | 0.38 | 0.5 | 0.073 | 0.083 | 0.092 | ||
| Vickers Vimy | human-engineered | 0.081 | 0.17 | 0.25 | 0.025 | 0.038 | 0.05 | ||
| Airbus A320 | human-engineered | 0.33 | 0.47 | 0.61 | 0.0078 | 0.0078 | 0.0078 | ||
| Boeing 747-400 | human-engineered | 0.39 | 0.61 | 0.83 | 0.0021 | 0.0021 | 0.0021 |
Table 1: Energy efficiency of flight for a variety of natural and man-made flying entities.
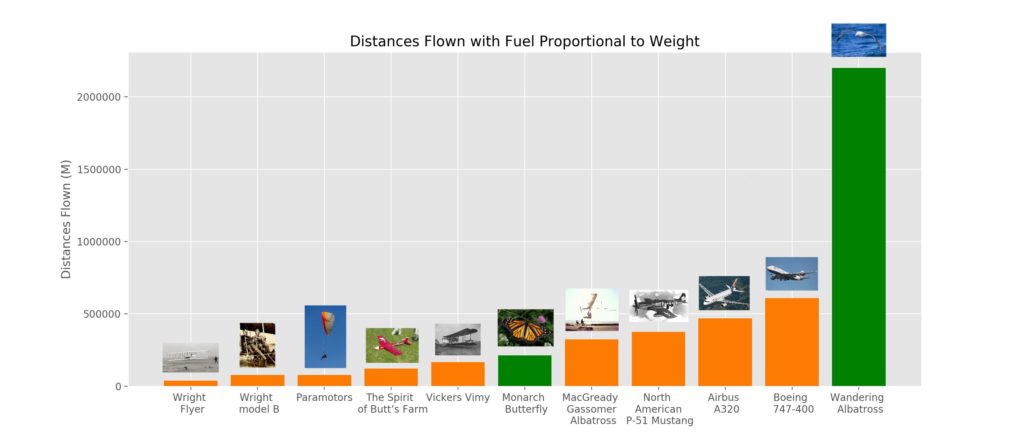
On mass⋅distance/energy, evolution beats engineers, but they are relatively evenly matched: the albatross (1.4-3.0 kg.m/J) and the Boeing 747-400 (0.39-0.83 kg.m/J) are the best in the natural and engineered classes respectively. Thus the best natural solution we found was roughly 2x-8x more efficient than the human-engineered one.2 We found several flying machines more efficient on this metric than the monarch butterfly.
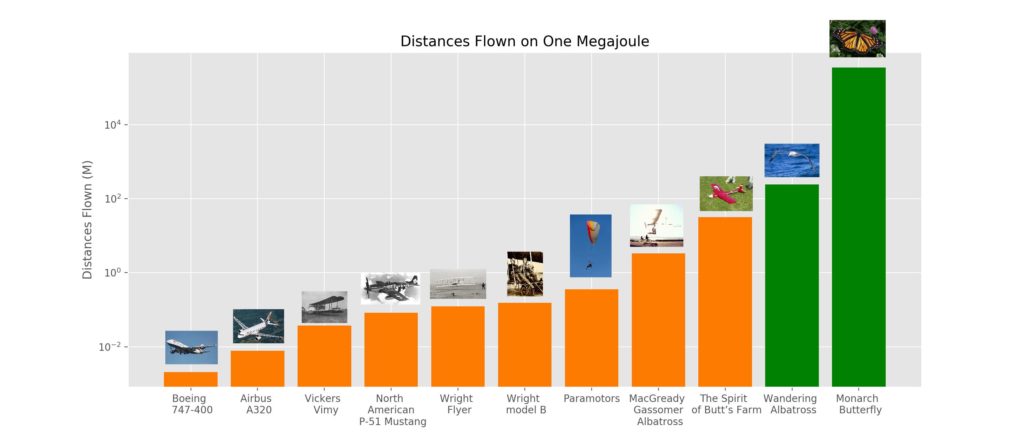
On distance/energy, the natural solutions have a much larger advantage. Both are better than all man-made solutions we considered. The best natural and engineered solutions respectively are the monarch butterfly (100,000-600,000 m/kJ) and the Spirit of Butts’ Farm (32 m/kJ), for roughly a 3,000x to 20,000x advantage to natural evolution.
Interpretation
We take this as weak evidence about the best possible distance/energy and distance.mass/energy measures achievable by human engineers or natural evolution. One reason for this is that this is a small set of examples. Another is that none of these animals or machines were optimized purely for either of these flight metrics—they all had other constraints or more complex goals. For instance, the paramotor was competing for a record in which a paramotor had to be used, specifically. For the longest human flight, the flying machine had to be capable of carrying a human. The albatross’ body has many functions. Thus it seems plausible that either engineers or natural evolution could reach solutions far better on our metrics than those recorded here if they were directly aiming for those metrics.
The measurements for distance.mass/energy covered a much narrower band than those for distance/energy: a factor of under two orders of magnitude versus around eight. Comparing best scores between evolution and engineering, the gap is also much smaller, as noted above (a factor of less than one order of magnitude versus three orders of magnitude). This seems like some evidence that that band of performance is natural for some reason, and so that more pointed efforts to do better on these metrics would not readily lead to much higher performance.
Primary author: Ronny Fernandez
Notes
- “Albatrosses and other large seabirds use dynamic soaring to gain sufficient energy from the wind to travel large distances rapidly and with little apparent effort.“
Richardson, Philip L., Ewan D. Wakefield, and Richard A. Phillips. “Flight Speed and Performance of the Wandering Albatross with Respect to Wind.” Movement Ecology 6, no. 1 (March 7, 2018): 3. https://doi.org/10.1186/s40462-018-0121-9.
See page on monarch butterflies for details of their soaring behavior.
- For the best case for engineers we compare the Boeing 747-400’s best score to the Albatross’s worst, and for the best case for evolution we do the opposite. This gives an advantage for evolution by a factor of somewhere between 1.7 and 7.7.