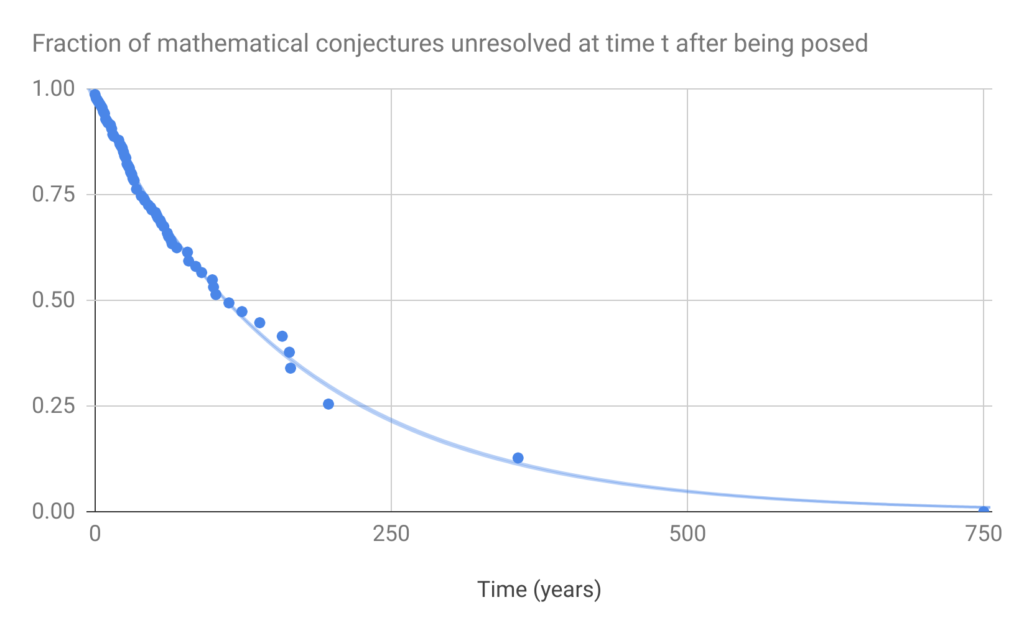
Conditioned on being remembered as a notable conjecture, the time-to-proof for a mathematical problem appears to be exponentially distributed with a half-life of about 100 years. However, these observations are likely to be distorted by various biases.
Support
In 2014, we found conjectures referenced on Wikipedia, and recorded the dates that they were proposed and resolved, if they were resolved. We updated this list of conjectures in 2020, marking any whose status had changed. We then used a Kaplan-Meier estimator1 to approximate the survivorship function.2
The results of this exercise are recorded here.3 Figure 1 below shows the survivorship function for the mathematical conjectures we found. The data is fit closely by an exponential function with a half-life of 117 years.4
Biases
We are using resolution times for remembered conjectures as a proxy for resolution times for all conjectures. Resolution time for remembered conjectures might be biased in several ways: old conjectures are perhaps more likely to be remembered if they are solved than if they are not, very recently solved conjectures are probably more likely to be remembered (though this only matters because the rate of conjecture posing has probably changed over time), and conjectures that were especially hard to solve might also be more notable. The latter hundred years contains few data points, which makes it particularly easy for it to be inaccurate.
Relevance
To the extent that open theoretical problems in AI are similar to math problems, time to solve math problems may be informative for forming a prior on time to solve AI problems.
Corresponding author: Asya Bergal
Notes
- “Kaplan–Meier Estimator.” Wikipedia. Wikimedia Foundation, April 1, 2020. https://en.wikipedia.org/w/index.php?title=Kaplan–Meier_estimator&oldid=948523181.
- “Survival Function.” Wikipedia. Wikimedia Foundation, October 8, 2019. https://en.wikipedia.org/w/index.php?title=Survival_function&oldid=920310453.
- The ‘Data’ tab of this spreadsheet contains the list of conjectures we used and their sources. The ‘Kaplan Meier’ tab contains the calculation of the survival function. The cell next to the cell marked ‘Exponential trendline’ contains our calculation for the exponential function fitting our Kaplan-Meier estimator.
- When fitting our exponential, we did not count the last point at 750 years, because it had a y-value of 0, which the Google Sheets LOGEST function would not accept when generating a best-fit curve. Nonetheless, Figure 1 suggests that the last point seems to fit our exponential reasonably well.