You Can’t Predict a Game of Pinball

Jeffrey Heninger, 29 March 2023

Introduction

When thinking about a new idea, it helps to have a particular example to use to gain intuition and to clarify your thoughts. Games are particularly helpful for this, because they have well defined rules and goals. Many of the most impressive abilities of current AI systems can be found in games.¹

To demonstrate how chaos theory imposes some limits on the skill of an arbitrary intelligence, I will also look at a game: pinball.

In this page, I will show that the uncertainty in the location of the pinball grows by a factor of about 5 every time the ball collides with one of the disks. After 12 bounces, an initial uncertainty in position the size of an atom grows to be as large as the disks themselves. Since you cannot launch a pinball with more than atom-scale precision, or even measure its position that precisely, you cannot make the ball bounce between the disks for more than 12 bounces.

The challenge is not that we have not figured out the rules that determine the ball’s motion. The rules are simple; the ball’s trajectory is determined by simple geometry. The challenge is that the chaotic motion of the ball amplifies microscopic uncertainties. This is not a problem that is solvable by applying more cognitive effort.

The Game

Let’s consider a physicist’s game of pinball.

Forget about most of the board and focus on the three disks at the top. Each disk is a perfect circle of radius R. The disks are arranged in an equilateral triangle. The minimum distance between any two disks is L. See Figure 1 for a picture of this setup.

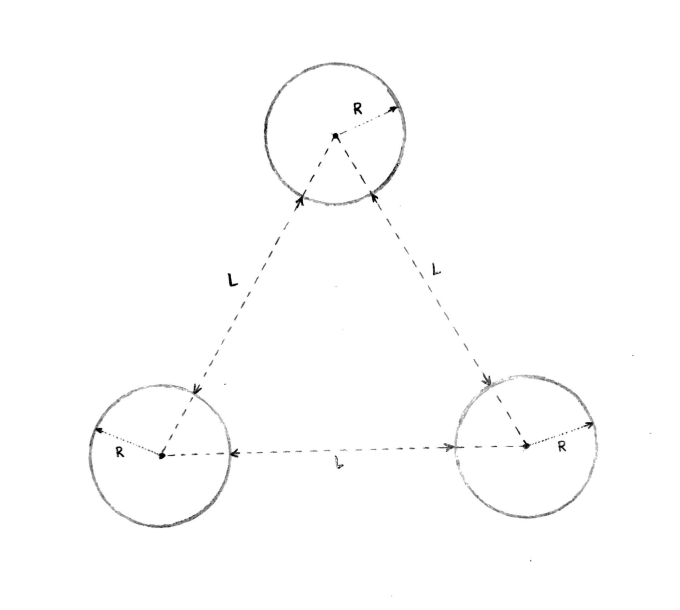
The board is frictionless and flat, not sloped like in a real pinball machine. Collisions between the pinball and the disks are perfectly elastic, with no pop bumpers that come out of the disk and hit the ball. The pinball moves at a constant speed all of the time and only changes direction when it collides with a disk.

The goal of the game is to get the pinball to bounce between the disks for as long as possible. As long as it is between the disks, it will not be able to get past your flippers and leave the board.

A real game of pinball is more complicated than this – and correspondingly, harder to predict. If we can establish that the physicist’s game of pinball is impossible to predict, then a real game of pinball will be impossible to predict too. 

Collisions

When the ball approaches a disk, it will not typically be aimed directly at the center of the disk. How far off center it is can be described by the impact parameter, b, which is the distance between the trajectory of the ball and a parallel line which passes through the center of the disk. Figure 2 shows the trajectory of the ball as it collides with a disk.

The surface of the disk is at an angle relative to the ball’s trajectory. Call this angle θ. This is also the angle of the position of the collision on the disk relative to the line through the center parallel to the ball’s initial trajectory. This can be seen in Figure 2 because they are corresponding angles on a transversal.

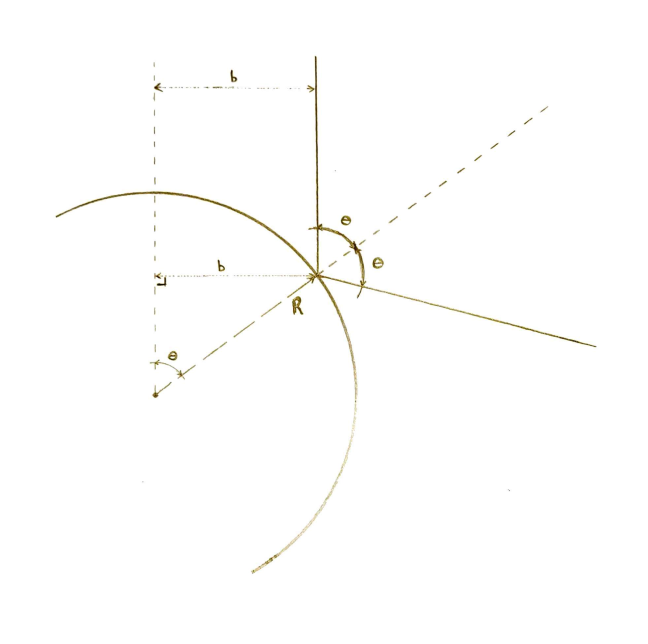
At the collision, the angle of incidence equals the angle of reflection. The total change in the direction of the ball’s motion is 2θ. 

We cannot aim the ball with perfect precision. We can calculate the effect of this imperfect precision by following two slightly different trajectories through the collision instead of one.

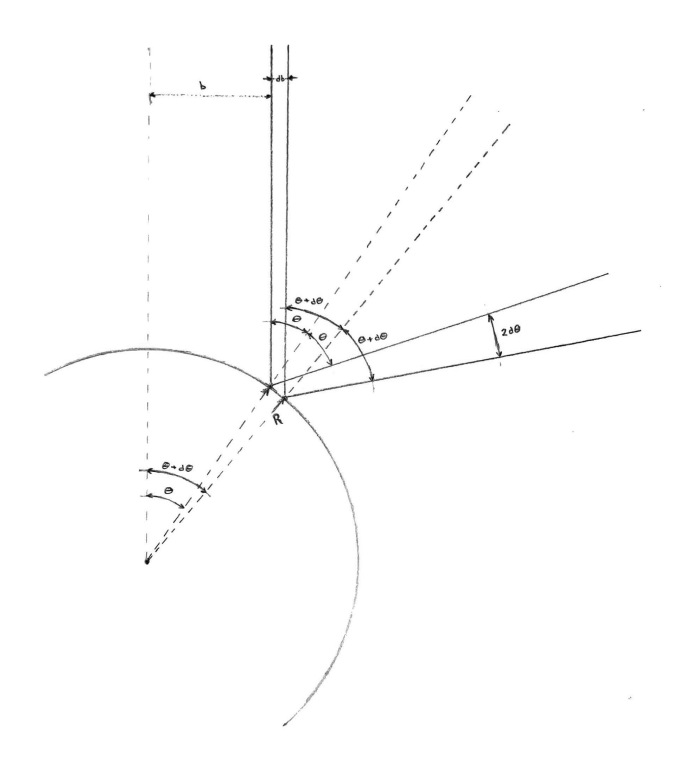
The two trajectories have slightly different initial locations. The second trajectory has impact parameter b + db, with db ≪ b. Call db the uncertainty in the impact parameter. We assume that the two trajectories have exactly the same initial velocity. If we were to also include uncertainty in the velocity, it would further decrease our ability to predict the motion of the pinball. A diagram of the two trajectories near a collision is shown in Figure 3.

The impact parameter, radius of the disk, and angle are trigonometrically related: b = R sinθ (see Figure 2). We can use this to determine the relationship between the uncertainty in the impact parameter and the uncertainty in the angle: db = R cosθ dθ.

After the collision, the two trajectories will no longer be parallel. The angle between them is now 2 dθ. The two trajectories will separate as they travel away from the disk. They will have to travel a distance of at least L before colliding with the next disk. The distance between the two trajectories will then be at least L 2 dθ.

Iteration

We can now iterate this. How does the uncertainty in the impact parameter change as the pinball bounces around between the disks?

Start with an initial uncertainty in the impact parameter, db₀. After one collision, the two trajectories will be farther apart. We can use the new distance between them as the uncertainty in the impact parameter for the second collision.² The new uncertainty in the impact parameter is related to the old one according to:

db_1 \geq L 2 d\theta = 2 L \frac{db_0}{R \cos\theta} \geq \frac{2L}{R} db_0 \,.

We also used 1 / cos θ > 1 for –π/2 < θ < π/2, which are the angles that could be involved in a collision. The ball will not pass through the disk and collide with the interior of the far side.

Repeat this calculation to see that after two collisions:

db_2 \geq \frac{2L}{R} db_1 \geq \left(\frac{2L}{R}\right)^2 db_0 \,,

and after N collisions,

db_N \geq \left(\frac{2L}{R}\right)^N db_0 \, .

Plugging in realistic numbers, R = 2 cm and L = 5 cm, we see that

db_N \geq 5^N \, db_0 \,.

The uncertainty grows exponentially with the number of collisions.

Suppose we had started with an initial uncertainty about the size of the diameter of an atom, or 10⁻¹⁰ m. After 12 collisions, the uncertainty would grow by a factor of 5¹², to 2.4 cm. The uncertainty is larger than the radius of the disk, so if one of the trajectories struck the center of the disk, the other trajectory would miss the disk entirely.

The exponential growth amplifies atomic-scale uncertainty to become macroscopically relevant in a surprisingly short amount of time. If you wanted to predict the path the pinball would follow, having an uncertainty of 2 cm would be unacceptable.

In practice, there are many uncertainties that are much larger than 10⁻¹⁰ m, in the production of the pinball, disks, & board and in the mechanics of the launch system. If you managed to solve all of these engineering challenges, you would eventually run into the fundamental limit imposed by quantum mechanics. 

It is in principle impossible to prepare the initial location of the pinball with a precision of less than the diameter of an atom. Heisenberg’s Uncertainty Principle is relevant at these scales. If you tried to prepare the initial position of a pinball with more precision than this, it would cause the uncertainty in the initial velocity to increase, which would again make the motion unpredictable after a similar number of collisions.

When I mention Heisenberg’s Uncertainty Principle, I expect that there will be some people who want to see the quantum version of the argument. I do not think that it is essential to this investigation, but if you are interested, you can find a discussion of Quantum Pinball in the appendix.

Predictions

You cannot prepare the initial position of the pinball with better than atomic precision, and atomic precision only allows you to predict the motion of the pinball between the disks with centimeter precision for less than 12 bounces. It is impossible to predict a game of pinball for more than 12 bounces in the future. This is true for an arbitrary intelligence, with an arbitrarily precise simulation of the pinball machine, and arbitrarily good manufacturing & launch systems.

This behavior is not unique to pinball. It is a common feature of chaotic systems.

If you have infinite precision, you could exactly predict the future. The equations describing the motion are deterministic. In this example, following the trajectory is a simple geometry problem, solvable using a straightedge and compass. 

But we never have infinite precision. Every measuring device only provides a finite number of accurate digits. Every theory has only been tested within a certain regime, and we do not have good reason to expect it will work outside of the regime it has been tested in.

Chaos quickly amplifies whatever uncertainty and randomness which exists at microscopic scales to the macroscopic scales we care about. The microscopic world is full of thermal noise and quantum effects, making macroscopic chaotic motion impossible to predict as well.

Conclusion

It is in principle impossible to predict the motion of a pinball as it moves between the top three disks for more than 12 bounces. A superintelligence might be better than us at making predictions after 8 bounces, if it can design higher resolution cameras or more precise ball and board machining. But it too will run into the low prediction ceiling I have shown here.

Perhaps you think that this argument proves too much. Pinball is not completely a game of chance. How do some people get much better at pinball than others?

If you watch a few games of professional pinball, the answer becomes clear. The strategy typically is to catch the ball with the flippers, then to carefully hit the balls so that it takes a particular ramp which scores a lot of points and then returns the ball to the flippers. Professional pinball players try to avoid the parts of the board where the motion is chaotic. This is a good strategy because, if you cannot predict the motion of the ball, you cannot guarantee that it will not fall directly between the flippers where you cannot save it. Instead, professional pinball players score points mostly from the non-chaotic regions where it is possible to predict the motion of the pinball.³

Pinball is typical for a chaotic system. The sensitive dependence on initial conditions renders long term predictions impossible. If you cannot predict what will happen, you cannot plan a strategy that allows you to perform consistently well. There is a ceiling on your abilities because of the interactions with the chaotic system. In order to improve your performance you often try to avoid the chaos and focus on developing your skill in places where the world is more predictable.

Appendix: Quantum Pinball

If quantum uncertainty actually is important to pinball, maybe we should be solving the problem using quantum mechanics. This is significantly more complicated, so I will not work out the calculation in detail. I will explain why this does not give you a better prediction for where the pinball will be in the future.

Model the disks as infinite potential walls, so the wave function reflects off of them and does not tunnel through them. If the pinball does have a chance of tunneling through the disks, that would mean that there are even more places the quantum pinball could be.

Start with a wave function with minimum uncertainty: a wave packet with Δx Δp =ℏ/2 in each direction. It could be a Gaussian wave packet, or it could be a wavelet. This wave packet is centered around some position and velocity.

As long as the wave function is still a localized wave packet, the center of the wave packet follows the classical trajectory. This can be seen either by looking at the time evolution of the average position and momentum, or by considering the semiclassical limit. In order for classical mechanics to be a good approximation to quantum mechanics at macroscopic scales, a zoomed out view of the wave packet has to follow the classical trajectory.

What happens to the width of the wave packet? Just like how the collisions in the classical problem caused nearby trajectories to separate, the reflection off the disk causes the wave packet to spread out. This can be most easily seen using the ray tracing method to solve Schrödinger’s equation in the WKB approximation.⁴ This method converts the PDE for the wave function into a collection of (infinitely many) ODEs for the path each ‘ray’ follows and for the value of the wavefunction along each ray. The paths the rays follow reflect like classical particles, which means that the region where the wave function is nonzero spreads out in the same way as the classical uncertainty would.

This is a common result in quantum chaos. If you start with a minimum uncertainty wave packet, the center of the wave packet will follow the classical trajectory and the width of the wave packet will grow with the classical Lyapunov exponent.⁵

After 12 collisions, the width of the wave packet would be several centimeters. After another collision or two, the wave function is no longer a wave packet with a well defined center and width. Instead, it has spread out so it has a nontrivial amplitude across the entire pinball machine. There might be some interesting interference patterns or quantum scarring,⁶ but the wave function will not be localized to any particular place. Since the magnitude of the wave function squared tells you the probability of finding the pinball in that location, this tells us that there is a chance of finding the pinball almost anywhere.

A quantum mechanical model of the motion of the pinball will not tell you the location of the pinball after many bounces. The result of the quantum mechanical model is a macroscopic wavefunction, with nontrivial probability of being at almost any location across the pinball machine. We do not observe a macroscopic wavefunction. Instead, we observe the pinball at a particular location. Which of these locations you will actually observe the pinball in is determined by wavefunction collapse. Alternatively, I could say that there are Everett branches with the pinball at almost any location on the board.

Solving wave function collapse, or determining which Everett branch you should expect to find yourself on, is an unsolved and probably unsolvable problem – even for a superintelligence.

Notes

1. Capabilities of state-of-the-art AI, 2023.
2. The collision also introduces uncertainty in the velocity, which we ignore. If we had included it, it would make the trajectory even harder to simulate.
3. The result is a pretty boring game. However, some of these ramps release extra balls after you have used them a few times. My guess is that this is the game designer trying to reintroduce chaos to make the game more interesting again.
4. Ray tracing was developed to reconcile the wave theory or light with the earlier successful theory which models light as rays coming from a point source. There is a mathematical equivalence between the two models.
5. I have found it difficult to find a source that explains and proves this result. Several people familiar with chaos theory (including myself) think that it is obvious. Here is a paper which makes use of the fact that a wave packet expands (or contracts) according to the classical Lyapunov exponent:
   Tomsovic et al. Controlling Quantum Chaos: Optimal Coherent Targeting. Physical Review Letters 130. (2023) https://arxiv.org/pdf/2211.07408.pdf.
6. Wikipedia: Quantum scar.