The computing power needed to replicate the human brain’s relevant activities has been estimated by various authors, with answers ranging from 1012 to 1028 FLOPS.
Details
Notes
We have not investigated the brain’s performance in FLOPS in detail, nor substantially reviewed the literature since 2015. This page summarizes others’ estimates that we are aware of, as well as the implications of our investigation into brain performance in TEPS.
Estimates
Sandberg and Bostrom 2008: estimates and review
Sandberg and Bostrom project the processing required to emulate a human brain at different levels of detail.1 For the three levels that their workshop participants considered most plausible, their estimates are 1018, 1022, and 1025 FLOPS.
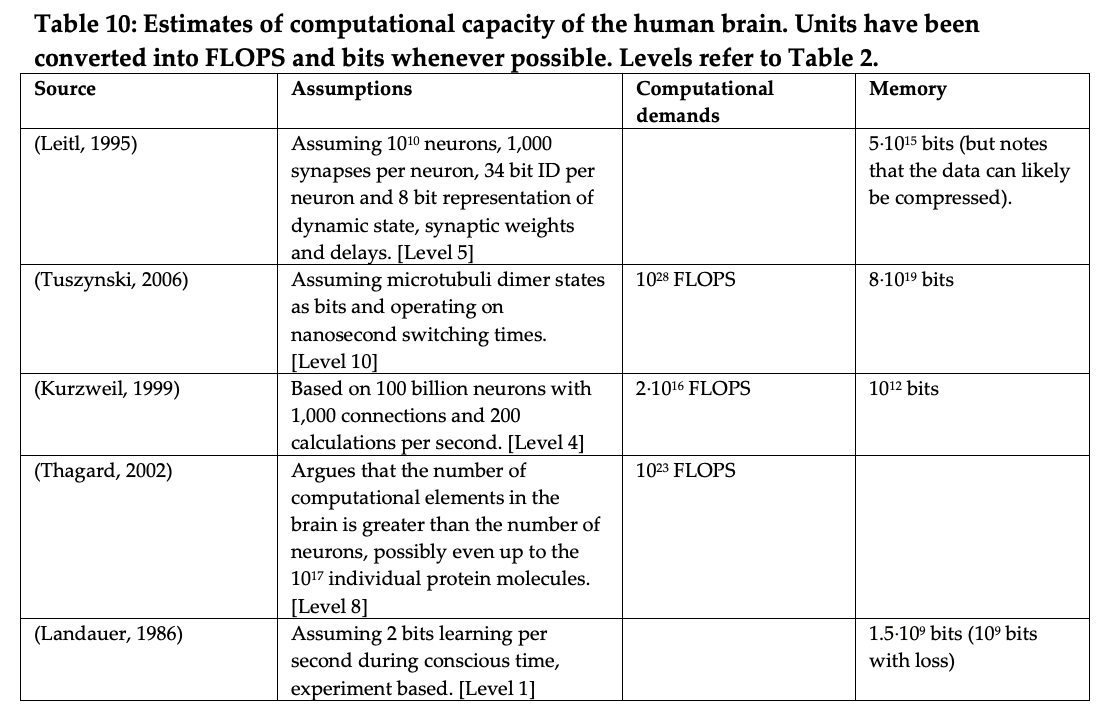
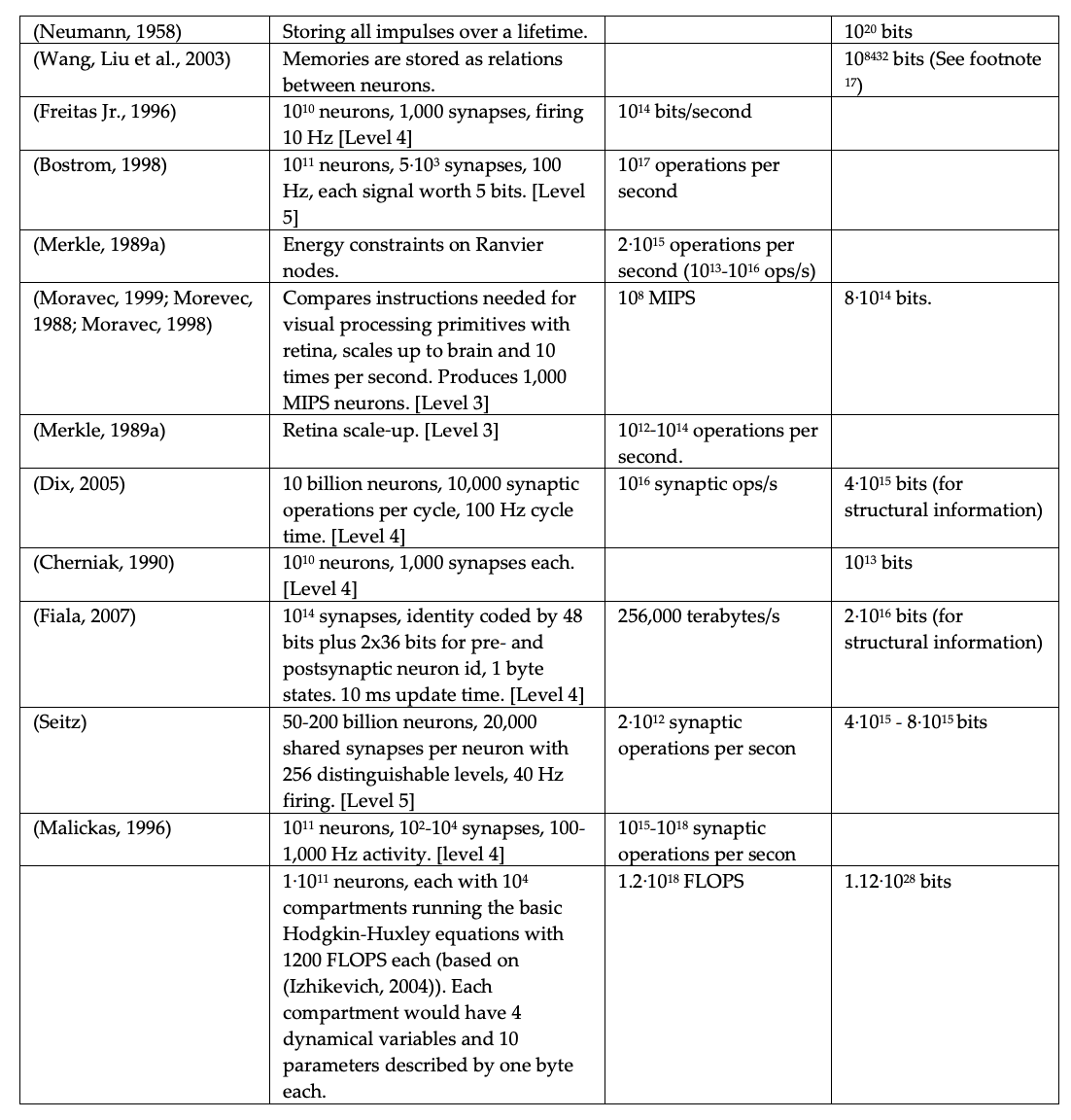
They also summarize other brain compute estimates, as shown below (we reproduce their Table 10).2 We have not reviewed these estimates, and some do not appear superficially credible to us.
Drexler 2018
Drexler looks at multiple comparisons between narrow AI tasks and neural tasks, and finds that they suggest the ‘basic functional capacity’ of the human brain is less than one petaFLOPS (1015).3
Conversion from brain performance in TEPS
Among a small number of computers we compared4, FLOPS and TEPS seem to vary proportionally, at a rate of around 1.7 GTEPS/TFLOP. We also estimate that the human brain performs around 0.18 – 6.4 * 1014 TEPS. Thus if the FLOPS:TEPS ratio in brains is similar to that in computers, a brain would perform around 0.9 – 33.7 * 1016 FLOPS.5 We have not investigated how similar this ratio is likely to be.
Notes
- From Sandberg and Bostrom, table 9: Processing demands (emulation only, human brain)(p80):
- spiking neural network: 1018 FLOPS (Earliest year, $1 million: commodity computer estimate: 2042, supercomputer estimate: 2019)
- electrophysiology: 1022 FLOPS (Earliest year, $1 million: commodity computer estimate: 2068, supercomputer estimate: 2033)
- metabolome: 1025 FLOPS (Earliest year, $1 million: commodity computer estimate: 2087, supercomputer estimate: 2044)
- See appendix A, Nick Bostrom and Anders Sandberg, “Whole Brain Emulation: A Roadmap,” 2008, 130.
- “Multiple comparisons between narrow AI tasks and narrow neural tasks concur in suggesting that PFLOP/s computational systems exceed the basic functional capacity of the human brain.”
- “The [eight] supercomputers measured here consistently achieve around 1-2 GTEPS per scaled TFLOPS (see Figure 3). The median ratio is 1.9 GTEPS/TFLOPS, the mean is 1.7 GTEPS/TFLOP, and the variance 0.14 GTEPS/TFLOP. ” See Relationship between FLOPS and TEPS here for more details
- 0.18 – 6.4 * 1014 TEPS =0.18 – 6.4 * 105 GTEPS =0.18 – 6.4 * 105 GTEPS * 1TFLOPS/1.9GTEPS = 9,000-337,000 TFLOPS = 0.9 – 33.7 * 1016FLOPS

Measuring brain performance in FLOPS is like measuring intelligence by trying to test only working memory capacity in an IQ test. Are you measuring in single or double precision? What is the width of the floating point register? Does each type of operation have an identical latency? Simply saying “FLOPS” is meaningless.
FLOPS is specifically a measure of floating point mathematical operations with a certain precision. While this measure may be important in determining the power required to *emulate* a brain (as statistical computations involve floating point numbers), that does not mean that a brain works in floating point values. In fact, it is easy to construct a system that does very little computation, but requires an insanely high amount of floating point operations to emulate it.
Emulating a biochemical system involves operating on floating point values, often with high precision. Emulating a CPU on the other hand may only need to use the APU for math. That does not mean an isolated system with 3 macromolecules and a couple thousand surrounding molecules does more meaningful computation than an old Zilog Z80 at 3.5 MHz, even though it takes a powerful computer with an extremely high FLOPS rating to emulate the biochemical system in real-time, whereas even an older embedded CPU from the early 2000s can perfectly emulate a Z80.
Furthermore, even for a computer, FLOPS is a very poor measurement of performance, as it only examines a single subsystem in a CPU, the FPU (floating point unit). A program using 100% of a processor may be spending very little of its time working the FPU. There are so many other subsystems in a CPU which make a difference, like the APU (arithmetic processing unit, which itself is split into multiple parts, like the multiplication engine and the addition engine), decoding engine, execution engine, crypto engine, cache system, register renaming engine, out-of-order/dependency execution engine or whatever it’s called, and much, much more. Simply doubling the FPUs on a CPU may double the FLOPS it can spit out, but a real-world workload may not be improved at all.
Not all floating point operations are the same. For a computer, two operations (with a few exceptions) are identical, and both will return in a predictable number of cycles. For a biological system (or literally *any* system that does not involve a fast and periodic clock source determining the rate of instruction execution, where a given instruction takes a fixed number of instructions), some instructions may be faster than others. What is 0.00000000000000000 divided by 1.000000000000000000 to 17 bit precision? A computer does this at the same speed as 0.000597012244189652 divided by 166892813.54003433 to 17 bits precision, simply because the division unit of the FPU (or the APU) is capable of answering *any* floating point question in a single cycle (a single cycle for a Nehelem Core 2).
For a biological system, there are many shortcuts that make some operations easier than others. A computer does not necessarily use these shortcuts because the limiting factor is the speed at which the fetching engine can read instructions from memory, and the speed at which the decoding engine can send the operations to the correct execution units. As the brain does not use fetching, decoding, and execution engines, FLOPS is a meaningless measurement.
Agree but would like to add that our (loosely used term) “software” does have a biological base (instinct autonomic). That part can be measured and given a base compute due to a repeatable base response program. It is also the smallest part. Our cerebrum with our neuroplasticity has some new revelations that may bring us back to drawing board and abandon hardware altogether. The science emerging within a neuron is converging with particle physics and quantum computing. It is possible that biology has a multitude of connections to a quantum field we have yet to fully observe. If that is the case silicon is doomed to be a just fantastic memorization and a bit of organized data merging and not ever truly think. If we somehow learn to connect the device to the quantum field we are connected to and in the same way, then we will face a challenge of our own making and hopefully not opened Pandora’s box.